Линейная регрессия
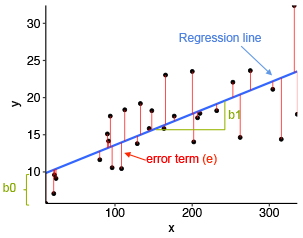
Линейная регрессия (или линейная модель) используется для прогнозирования количественной переменной результата (y) на основе одной или нескольких переменных — предикторов (x).
Цель состоит в том, чтобы построить математическую формулу, которая определяет y как функцию переменной x. После того, как мы создали статистически значимую модель, ее можно использовать для прогнозирования будущих результатов на основе новых значений x.
Когда вы строите регрессионную модель, вам необходимо оценить производительность прогностической модели. Другими словами, вам нужно оценить, насколько хорошо модель предсказывает результаты новых тестовых данных, которые не использовались для построения модели.
Для оценки эффективности модели прогнозной регрессии обычно используются две важные метрики:
Среднеквадратичная ошибка — RMSE, которая измеряет ошибку прогнозирования модели. Это соответствует средней разнице между наблюдаемыми известными значениями результата и прогнозируемой величиной по модели. RMSE рассчитывается как.
[code lang=»R»]RMSE = mean((observeds — predicteds)^2) sqrt()[/code]
Чем ниже RMSE, тем лучше модель.
Для вычисления (Mean Square Error) ошибки (MSE) все остатки регрессии возводятся в квадрат, суммируются и сумма делится на общее число ошибок:
![]()
Квадратный корень из данной величины обозначается как RMSE (Root Mean Square Error):

R-квадрат — коэффициент детерминации , представляющий квадратную корреляцию между наблюдаемыми известными значениями результата и прогнозируемыми значениями модели.
Коэффициент детерминации (R2) рассматривают, как правило, в качестве основного показателя, отражающего меру качества регрессионной модели, описывающей связь между зависимой и независимыми переменными модели. R2 рассчитывается по формуле:

R2 показывает, какую часть изменчивости наблюдаемой переменной можно объяснить с помощью построенной модели, иначе говоря — значение коэффициента детерминации определяет долю (в процентах) изменений, обусловленных влиянием факторных признаков, в общей изменчивости результативного признака.
Значение R2 должно находиться в диапазоне от нуля до единицы: 0 ≤ R2 ≤ 1. Модель считается более качественной, если значение коэффициента детерминации близко к 1. Если R2=1, то эмпирические точки (xi; yi) лежат точно на линии регрессии и между переменными Y и Х существует линейная функциональная зависимость. Если R2=0, то вариация зависимой переменной полностью обусловлена неучтенными в модели факторами.
Чем выше R2, тем лучше модель.
Простой рабочий процесс для построения модели прогнозной регрессии выглядит следующим образом:
1. Случайно разделите ваши данные на тренировочный набор (80%) и тестовый набор (20%)
2. Постройте регрессионную модель, используя обучающий набор
3. Делайте прогнозы, используя набор тестов, и вычисляйте метрики точности модели.
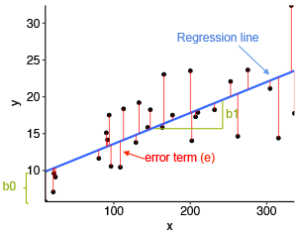
Математическая формула линейной регрессии может быть записана следующим образом:
y = b0 + b1*x + e
Когда у вас есть несколько переменных предиктора, уравнение можно записать в виде y = b0 + b1*x1 + b2*x2 + … + bn*xn, где:
b1, b2,…, bn — веса или коэффициенты регрессии, связанные с предикторами x1, x2,…, xn.
*
e — ошибки (также известным как остаточные ошибки ), часть y, которая может быть объяснена регрессионной моделью
Здравствуйте. А на сколько эти методы применимы, скажем, для прогноза в ставках на спорт? Есть ли готовые примеры на R?